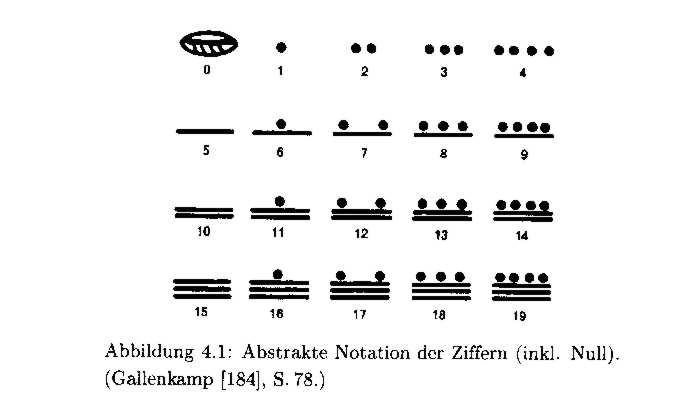
Das Zahlensystem der Maya (IV)

Es enthält die 0 (null), und die Zahlen, die von 1 bis vier als Punkte dargestellt werden, die 5 als Querstrich, dann die 20 wieder als Punkt etc.

Eine weitere Darstellung der Zahlen wurde mit Glyphen erreicht.

Auf der untersten Ebene (Linie) werden die Zahlen bis 20 angeschrieben; auf der 2. Ebene und jeder weiter höheren Ebene bezeichnen die Zeichen dann jeweils ein 20-faches ihres Wertes.

Somit steht auf Ebene 2 der Punkt für 20, auf Ebene 3 für 400 und auf Ebene 4 für 8000. Die obere Grafik verdeutlicht dies.

Ein weiteres Rechenexempel:

Das Berechnen von Kalenderdaten

Wenn Datumsdistanzen errechnet werden sollen, ergeben sich aus der Mayadarstellung der Zahlen folgende Berechnungsmöglichkeit:

Wir haben z.B. im Dresdner Codex auf der Seite 24 folgende Berechnung durchzuführen: auf ein Datum 12.19.13-16-0 soll 6-2-0 (2200d) hinzuaddiert werden. Daraus folgt dann: 13.0.0-0-0 4 Ahau 8 Cumku.

Die Zahl 6-2-0 wird von rechts nach links gelesen: zuerst die Tage (kin) = 0d, dann die Monate (uinal) = 2 = 2 x 20d = 40d und schließlich die Jahre (tun) = 6 = 360d x 6 = 2160d. Das ergibt dann 2160 + 40 + 0 = 2200d.

Eine weitere Berechnung verlangt immer 8-2-0 aufzuaddieren. Das sind 2920d und sieht folgendermaßen aus: 16-4-0, 1.4-6-0, 1.12-8-0, etc. (bezüglich der Reihenfolge siehe die Seite "Der Kalender der Mayas (I)").

Ein Maya-Datum besteht also aus den Distanzzahlen vom Datumsbeginn aus gerechnet und den Tzolkin- und Haabbenennungen:

zurück zur Mayaseite 

back / zurück   

Copyright (c) 2004 by A. Klaudius.  All Rights Reserved